См. другие научно-популярные вебстраницы и сайты автора:
Бильярдная игра на протяжении всей её многовековой истории
стимулировала научные исследования в механике и математике. Гюстав
Гаспар Кориолис известен тем, что дал окончательную
формулировку теории относительного движения, введя понятия о так называемых силе и ускорении Кориолиса. Однако самой любимой
работой Кориолиса была книга «Математическая теория явлений бильярдной игры»,
которую он написал в 1835 году. Анализ соударений шаров с кием, между собой и
бортами бильярдного стола позволял проверять «обкатывать» известные законы
механики и предлагать новые. Бильярдная игра возбуждала умы не только физиков,
но и математиков, которые с энтузиазмом стали изучать ломаную,
вдоль которой движется шар по бильярдному столу. При этом у математиков
бильярдный стол часто превращался из прямоугольного в
треугольный, эллиптический и т.п. Обо всех этих математических бильярдах в
увлекательной форме написано в книге Г.А. Гальперина и А.Н. Землякова (выпуск
77 библиотечки «Квант», 1990 г).
Существует более десятка разновидностей бильярда: русская пирамида,
американка, пул, снукер и другие. В карамболи, одной из игр в бильярд, нет даже
луз для шаров. А мы попробуем пойти ещё дальше и предложим играть в бильярд без
луз на очень узком столе – шириной в диаметр одного шара. По такому бильярдному
столу шары смогут двигаться только вдоль одной прямой. Таким образом, мы
понизили размерность игры – с двухмерной до
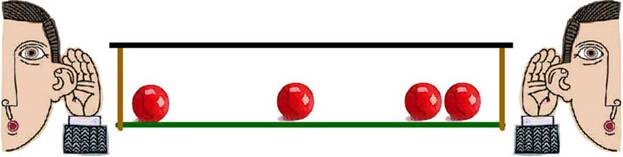
одномерной. Поэтому и назовём придуманный нами бильярд «одномерным» (см. рис.1).
Рисунок 1. Одномерный бильярд.
При игре в обычный «двухмерный» бильярд никто не следит за тем, с какой частотой стучат мячи по бортам стола. Всех волнует результат – сколько шаров оказалось в лузах. В одномерном бильярде луз нет, и единственное, что можно считать – столкновения шаров между собой и с торцевыми бортами стола. Для простоты предположим, что трение между шарами и столом отсутствует, а удары между шарами и бортами стола абсолютно упругие. В таких условиях начавшееся движение шаров никогда не прекратится и станет постоянным источником своеобразной чечётки - периодического постукивания шаров о торцевые стенки одномерного бильярда.
Пусть в одномерный бильярд, закрытый сверху непрозрачной крышкой, играют два игрока. С помощью кия или другого специального устройства, привёдём в движение шары и попросим игроков разгадать следующие загадки одномерного бильярда:
1. от чего зависит средняя частота постукивания крайних шаров о торцы бильярда?
2. как можно определить, сколько шаров внутри одномерного бильярда?
3. если шары разной массы, то, как можно найти, во сколько раз отличаются массы крайних шаров?
4. что общего между одномерным бильярдом и пружиной?
Кто первым разгадает эти загадки, тот и выиграл! При ответе на вопросы можно пользоваться компьютером и измерять интервалы между последовательными столкновениями крайних шаров с торцами бильярда с помощью любых подслушивающих устройств.
Определим физические характеристики стола и шаров для игры в одномерный бильярд. Чтобы стол было легко взять и встряхнуть находящиеся на нём шары, пусть его длина L = 1 м. Шары для бильярда сначала делали из слоновой кости, а потом, когда людям и слонам это не понравилось, стали делать из других материалов с такой же плотностью (1900 кг/м3) и механическими свойствами. Обычные шары имеют диаметр 50-60 мм и массу 150 – 200 г. Чтобы «облегчить» себе игру возьмём шары диаметром D = 30 мм с массой m = 25 г. Будем считать также, что в начале игры специальное устройство передаёт одному, нескольким или всем шарам энергию, общая величина которой всегда постоянна и равна Е0 = 2 мДж. Если эта энергия передаётся только одному шару массой 25 г, то он начинает двигаться со скоростью 0,4 м/с. Итак, начинаем играть в одномерный бильярд.
Когда одному всё, а другим ничего
Пусть в одномерном бильярде размещены N шаров одинаковой массы, и мы приводим их в движение с помощью кия, ударив только по одному из них (битку) и придав ему начальную скорость v0. В этом случае при каждом столкновении шаров энергия движущегося шара будет целиком передаваться покоящемуся, в результате чего ранее двигавшийся шар остановится, передав эстафету следующему. Легко показать, что в таких условиях постукивание крайних шаров по торцам стола будет ритмичным, c интервалом T, равным:
Однако абсолютно одинаковые по массе шары сделать невозможно, и поэтому правила разрешают играть в бильярд комплектом шаров, если их масса отличается не более чем на 10 %. Интересно, как измениться формула (1), если в одномерный бильярд играть шарами, масса которых варьирует в пределах 5 - 10 %? Первый ответ, который приходит в голову – интервалы T между ударами крайних шаров с бортами стола при не очень одинаковых массах будут слегка изменяться во времени, но всё же среднее значение Т можно будет вычислять по формуле (1). Чтобы ответить на этот вопрос точно, смоделируем игру в бильярд на компьютере.
Задача о столкновения двух шаров одинакового размера с массой m1 и m2, движущихся вдоль одной прямой без трения очень проста. Если, v1 и v2 – проекции скоростей шаров 1 и 2 на ось, вдоль которой они движутся, до столкновения, то после абсолютно упругого удара их скорости v1N и v2N можно найти с помощью следующих формул:
применяя которые для каждого столкновения можно следить за скоростью шаров, а значит, и за их положением в одномерном бильярде.
Положим в одномерный бильярд
3 шара, масса которых составляет 25, 23 и 27 грамм и ударим средний шар (биток),
придав ему энергию 2 мДж (v0
= 0,417 м/с).
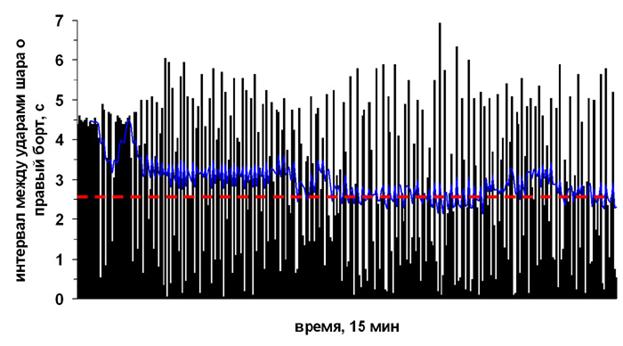
Рисунок 2. Интервалограмма ударов правого мяча по торцу одномерного
бильярда при небольшом неравенстве находящихся в нём трёх мячей. Обратите
внимание на постепенное учащение ударов. Синяя кривая – усреднённые значения по
соседним 8 точкам. Остальные условия компьютерного моделирования см. в тексте.
На рис.2 показано, как, по мнению компьютера, будут изменяться интервалы Т между соударениями правого шара со стенкой (интервалограмма). Видно, что Т изменяются в довольно широком диапазоне, гораздо большем, чем 10 %. Таким образом, наши ощущения нас обманули. Приблизительно такая же картина имеет место, когда разброс в массе шаров ещё меньше (25, 24, 26 г).
Судить о том, как изменяется среднее значение Т со временем по интервалограмме, изображённой на рис.2, очень трудно. Поэтому на том же рисунке изображена синяя кривая, показывающая, как изменяется среднее значение Т при усреднении 8 соседних интервалов. Видно, что в самом начале средний интервал составлял около 4,5 с, что очень близко к величине, даваемой формулой (1). Однако со временем среднее значение Т постепенно уменьшается, испытывая заметные колебания, достигая значений, близких к 2,5 с. То же происходит и для другого числа шаров. При этом, чем больше число шаров, тем быстрее средняя величина Т оказывается меньше той, которую можно вычислить с помощью (1).
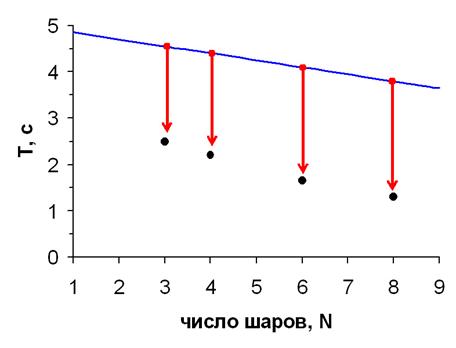
Рисунок 3. Среднее значение интервала, Т между соударениями крайних шаров со стенкой (жирные точки) в реальных условиях, когда массы шаров слегка отличаются. Синей прямой показана зависимость, даваемая формулой (1).
На рисунке 3 показано, каких величин достигает среднее значение Т для различного числа шаров (чёрные точки) через 10-15 минут игры. Для сравнения на том же рисунке показана прямая, соответствующая формуле (1). Итак, формула (1) может давать оценку среднего значения Т при незначительной вариации масс шаров только в самом начале игры. Чтобы выяснить, почему формула (1) не работает уже через несколько минут, рассмотрим, как передаётся энергия от шара к шару при неравенстве их масс.
Если массы сталкивающихся шаров разные, то движущейся шар никогда не сможет передать всю свою энергию покоящемуся, и после столкновения оба этих шара будут обладать энергией. Таким образом, неравенство масс сталкивающихся шаров всегда приводит к тому, что энергия «размазывается» между шарами. Поэтому после достаточного числа столкновений шаров, обладающих разной массой, средняя энергия каждого из них становится близкой к Е0/N, где Е0 - первоначальная энергия битка, а N – число шаров.
Делёж энергии и стук по бортам
Мы доказали, что формула (1) справедлива только в идеальных случаях – когда массы шаров абсолютно одинаковы. А такого никогда не бывает, и сталкивающиеся шары со временем делят энергию между собой поровну. Но остаётся непонятным, почему этот делёж энергии всегда сопровождается уменьшением среднего интервала постукивания крайних шаров по бортам? А верно ли это для всяких вариантов перераспределения энергии между шарами? Может быть, зависимость среднего интервала постукивания от «дележа» гораздо более сложная?
Чтобы ответить на эти вопросы опять обратимся к помощи компьютера и поиграем в одномерный бильярд с двумя шарами абсолютно одинаковой массы, разделяя с самого начала энергию между ними так, как нам захочется. Так как каждое столкновение шаров с одинаковой массой приводит просто к обмену энергий, то со временем распределение энергий в такой системе не меняется. Поэтому на такой системе можно выяснить, как зависит средняя величина T от отношения энергий шаров.
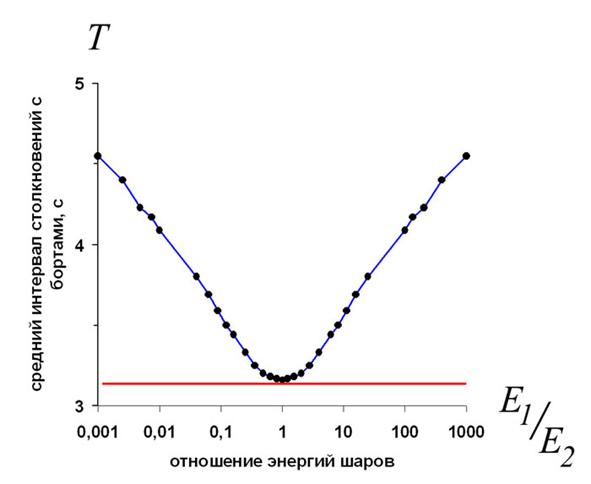
Рисунок 4. Зависимость среднего интервала столкновений с бортом от отношений энергий шаров для одномерного бильярда с двумя шарами одинаковой массы.
На рисунке 4 показаны результаты моделирования игры в одномерный бильярд с двумя шарами одинаковой массы при различных отношениях их энергий (Е1/Е2) и условии, что Е1 + Е2 = 2 мДж. Видно, что при увеличении отношения Е1/Е2 средний интервал Т столкновений шара с бортом бильярда монотонно уменьшается, достигая минимума при Е1/Е2 = 1. Как следует из результатов моделирования, при абсолютно несправедливом распределения энергии (Е1/Е2 = 0 и Е1/Е2 = ¥) интервал Т = 4,55 с, что соответствует формуле (1), однако, при переходе к справедливому распределению (Е1/Е2 = 1) средний интервал Т уменьшается до 3,16 с.
Вычислить среднюю величину Т при Е1/Е2 = 1 можно
и без помощи компьютера. Так как энергию шары поделили поровну, то скорость
каждого из них будет равна 
, где v0
та же, что и в формуле (1). Предположим теперь, что оба шара одновременно
начинают движение от торцов одномерного бильярда к середине. Очевидно, что встретившись в середине стола, они оттолкнутся друг от
друга и с той же скоростью продолжат движение обратно к бортам. Легко показать,
что в таких условиях интервал Т между их
соударениями с бортом составит:
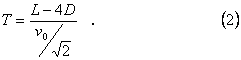
Подставляя в (2) L = 1 м, D = 0,03 м,
v0 =
0,4 м/с, получаем T =3,11 с, что довольно близко к результату компьютерного
моделирования (T = 3,16 с). Сравнивая формулу (1) для N=2 c формулой
(2) замечаем, что уменьшение Т произошло из-за того, что путь проходимый
шарами между столкновениями с торцами уменьшился в два раза, а скорость шаров – в 
. В результате, интервал столкновений с бортами для самого
справедливого распределения энергий уменьшился в . При менее
справедливых отношениях (0 <Е1/Е2 <1) происходит
то же самое – путь между столкновениями со стенкой падает быстрее, чем скорость
шаров, однако, найти аналитическое выражение, описывающее зависимость,
изображённую на рис.4, автору не удалось. Пытливый читатель может попробовать
здесь свои силы!
Делим энергию поровну и разгадываем вторую загадку
Итак, при любом начале игры в одномерный бильярд через несколько минут реальные шары поделят энергию между собой так, что средняя энергия каждого из них будет равна Е0/N, где Е0 – суммарная энергия всех шаров, а N – число шаров. Теперь мы можем разгадать вторую загадку одномерного бильярда – узнать, сколько шаров внутри. Попросим компьютер сыграть в бильярд различным числом шаров – от 2 до 9, и каждый раз через 15 минут измерим средний интервал Т постукивания шаров в торцы стола (см. рис.5).
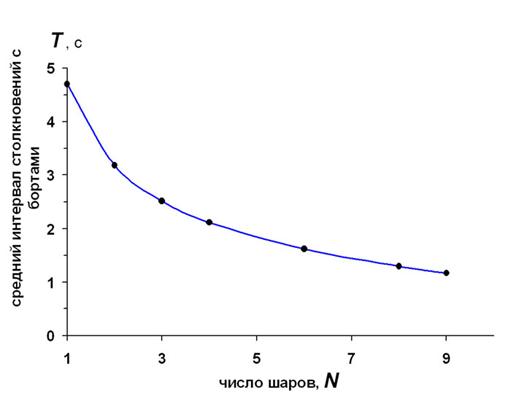
Рисунок 5. Зависимость среднего интервала постукивания, Т от числа шаров, N в одномерном бильярде
На рисунке 5 показаны результаты компьютерного моделирования при изначально «справедливом» распределении энергии между шарами равной массы. Видно, что при этих условиях средний интервал постукивания падает гораздо быстрее с увеличением числа шаров, чем это предсказывает формула (1). Кривая, изображённая на рис.5, даёт возможность отгадать вторую загадку одномерного бильярда - надо лишь измерить среднее значение Т, а потом по этой кривой найти соответствующее N. При этом, однако, имейте ввиду, что полученная зависимость справедлива только для выбранных параметров бильярда (L = 1 м, D = 0,03 м, Е0 = 2 мДж). Очевидно, что для Е0 > 2 мДж эта кривая пройдёт ниже, т.к. средняя скорость движения шаров будет больше. Наоборот, меньший диаметр шаров (D < 0,03 м) сдвинет кривую вверх, т.к. увеличит путь проходимый шарами между столкновениями. Конечно, хотелось бы вывести аналитическое выражение, связывающее T, L, D и Е0, но нам пока это не по силам. Да, и вообще, мы опять забыли о массе шаров.
Золотой шар в одномерном бильярде
Пусть кто-то из богатых шутников вместо одного из трёх обычных шаров положил в бильярдный стол золотой шар, закрыл стол крышкой и запустил движение шаров, придав им суммарную энергию Е0. Можно ли определить, где находится этот золотой шар – сбоку или посередине, прослушивая чечётку столкновений крайних шаров с торцами одномерного бильярда?
Так как плотность золота в 10 раз больше плотности слоновой кости, то золотой шар диаметром 3 см должен иметь массу 250 г. Поставим золотой шар между обычными и попросим компьютер поиграть в такой одномерный бильярд, распределив поровну энергию между шарами. Интервалограммы левого и правого обычных шаров, показаны на рис.6а и б, соответственно.
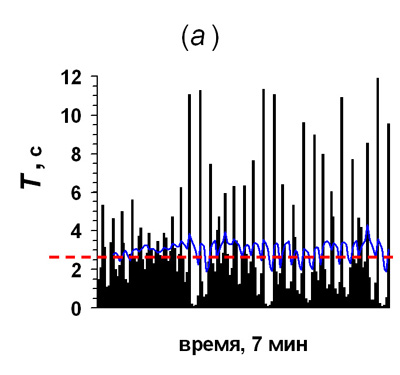
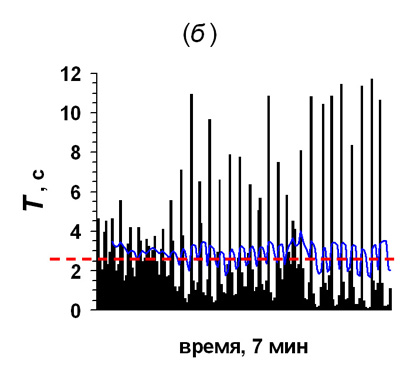
Рисунок 6. Интервалограммы левого (а) и правого (б) шаров
одномерного бильярда, между которыми находится золотой шар. Видно, что наличие
между ними тяжёлого шара не влияет на средний интервал столкновений.
Как следует из интервалограмм, изображённых на рис.6, средние значения T для левого и правого шаров (голубые кривые на панелях а и б) колеблются вблизи 2,5 с, что соответствует Т для трёх одинаковых шаров (см. рис.5). Таким образом, если золотой шар находится между обычными, то, прислушиваясь к постукиваниям крайних шаров, обнаружить его не удастся.
Золотой шар – крайний
Если положить золотой шар не между обычными, а с краю, и повторить компьютерную игру в одномерный бильярд с тремя шарами, то окажется, что частота постукивания золотого шара о торец будет гораздо меньше, чем обычного шара, находящегося с другой стороны (см. рис.7). Видно, что средний интервал постукивания левого (обычного) шара опять варьирует вокруг 2,5 с, однако правый (золотой) ударяется о торец гораздо реже – в среднем один раз в 8,7 с. Таким образом, если известно, что золотой шар с краю, то, сравнивая постукивания крайних шаров, можно найти с какой он стороны – там, где удары реже. Вот, мы и начали разгадывать третью загадку одномерного бильярда. Оказывается, что если крайние шары разной массы, то, чем меньше масса шара, тем чаще он стучит о борт. Но верно ли это для любого числа шаров?
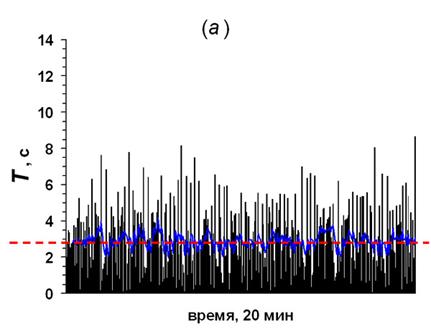
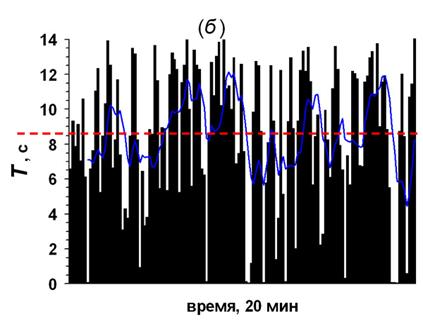
Рисунок 7. Интервалограмма столкновений левого (обычного) шара (а)
и правого (золотого, б) при игре в одномерный бильярд в три
шара. Видно, что золотой шар сталкивается с бортом гораздо реже, чем обычный.
Масса крайнего шара и средняя частота ударов о борт
Чтобы выяснить зависимость средней частоты ударов крайних шаров от
их массы, проведём несколько компьютерных экспериментов, в которых будем
изменять массу правого крайнего шара, оставляя неизменной массу левого
крайнего. Пусть число шаров будет равно опять трём, чтобы полученный результат
с золотым шаром не пропал. На рисунке 8 показано, как увеличивается средний
интервал постукивания правого шара с увеличением его массы, mПР.
Пунктирной кривой показана аппроксимация этой зависимости функцией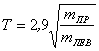 
. Таким образом, из результатов моделирования следует,
что период соударений правого шара должен быть пропорционален квадратному корню
из его массы.
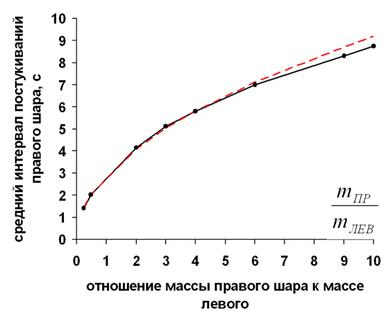
Рисунок 8. Зависимость среднего интервала постукивания правого шара
от отношения его массы, mПР к массе
левого, mЛЕВ.
Компьютерное моделирование одномерного бильярда с тремя шарами.
Аналогичные эксперименты были поставлены автором для другого числа шаров, N – от 4 до 9, и везде была обнаружена квадратичная зависимость. Попробуем найти причину этой зависимости и наконец вывести формулу, по которой можно вычислять T, зная N, m и Е0.
Формула для периода колебаний «пружины одномерного бильярда»
Как мы уже убедились, реальные шары в
одномерном бильярде стараются разделить энергию поровну. Очевидно, что и
среднее расстояние, которое проходит каждый шар из N шаров между
соударениями, тоже является только N-ой долей длины бильярда. Другими
словами, средняя длина свободного пробега каждого шара составляет 
. Поэтому средний интервал Т между соударениями крайнего шара со стенкой равен:
где vСР – средняя скорость движения данного шара. Если суммарная энергия всех шаров бильярда равна Е0, и она разделена поровну между ними, то, очевидно,
где m – масса данного шара. Подставляя (4) в (5), получаем долгожданную формулу:
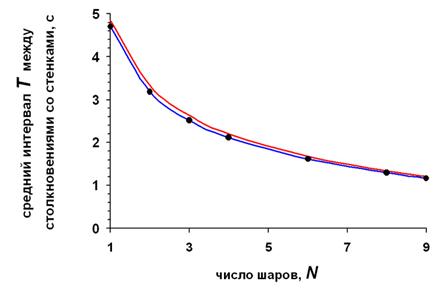
Рисунок 9. Теоретическая зависимость среднего интервала
столкновений со стенками бильярда (красная), построенная по формуле (5) и
результаты компьютерного моделирования (синяя).
На рис.9 красная кривая, построенная по формуле (5), наложена на экспериментальные данные, полученные при моделировании. Видно, что формула (5) описывает чечётку одномерного бильярда достаточно точно.
Так как формула (5) своей зависимостью Т от 
очень напоминает
формулу для периода колебаний пружинного маятника, преобразуем её следующим
образом:
где kОБ – эквивалентная жёсткость одномерного бильярда.
Как следует из формулы (6), крайний шар воспринимает остальную часть бильярда как пружину с жёсткостью kОБ. При этом, чем большая суммарная энергия шаров и их число, тем больше жёсткость такой «бильярдной» пружины.
Загадка одномерного бильярда для читателя
Вот, мы и разгадали четыре загадки одномерного бильярда. Конечно, их гораздо больше, и ещё одну из них я сейчас загадаю, а любознательный читатель уже без моей помощи наверняка найдёт правильный ответ. Вот она.
Как мы уже узнали, средняя частота ударов крайнего шара о торец бильярда не зависит от того, какие шары находятся рядом с ним, а определяется только массой данного шара, суммарной энергией всех шаров, их числом N и геометрическими размерами. Для N = 3 найдите алгоритм, с помощью которого, прослушивая чечётку крайнего шара о торец бильярда, можно качественно оценить массу среднего шара. Другими словами, надо определить, масса среднего шара существенно (в несколько раз) больше или меньше, чем у крайнего шара. Удачи Вам!
 |
Издательство "Просвещение" в 2008 году выпустило мою новую научно-популярную книжку Не только о физике яйца, в которой действие законов физики показано в будничных фактах и явлениях. |
 |
В 2008 году издательство "Просвещение" выпустило написанный мною учебник фиксированного формата, входящий в учебно-методический комплект "Архимед". |
Оставить отзыв в ГОСТЕВОЙ книге
